Basic nuclear properties – Size, shape, charge distribution, spin and parity
The nucleus consists of the elementary particles, protons and neutrons which are known as nucleons. A proton has positive charge of the same magnitude as that of electron and its rest mass is about 1836 times the mass of an electron. A neutron is electrically neutral, whose mass is almost equal to the mass of the proton. The nucleons inside the nucleus are held together by strong attractive forces called nuclear forces.
The nucleus consists of the elementary particles, protons and neutrons which are known as nucleons. A proton has positive charge of the same magnitude as that of electron and its rest mass is about 1836 times the mass of an electron. A neutron is electrically neutral, whose mass is almost equal to the mass of the proton. The nucleons inside the nucleus are held together by strong attractive forces called nuclear forces.
A nucleus of an element is represented as ZXA, where X is the chemical symbol of the element. Z represents the atomic number which is equal to the number of protons and A, the mass number which is equal to the total number of protons and neutrons. The number of neutrons is represented as N which is equal to A−Z. For example, the chlorine nucleus is represented as 17Cl35. It contains 17 protons and 18 neutrons.
Nuclear size:
According to Rutherford’s α−particle scattering experiment, the distance of the closest approach of α − particle to the nucleus was taken as a measure of nuclear radius, which is approximately 10−15m. If thenucleus is assumed to be spherical, an empirical relation is found to hold good between the radius of the nucleus R and its mass number A.It is given by
Atomic mass unit:
Nuclear size:
According to Rutherford’s α−particle scattering experiment, the distance of the closest approach of α − particle to the nucleus was taken as a measure of nuclear radius, which is approximately 10−15m. If thenucleus is assumed to be spherical, an empirical relation is found to hold good between the radius of the nucleus R and its mass number A.It is given by
R ∝ A1/3 R = roA1/3
where ro is the constant of proportionality and is equal to 1.3 F(1 Fermi, F = 10−15 m)
Nuclear density:
The nuclear density ρN can be calculated from the mass and size of the nucleus.
ρN =Nuclear mass/Nuclear volume
Nuclear mass = AmN where, A = mass number and mN = mass of one nucleon and
is approximately equal to 1.67 × 10−27 kg
Nuclear volume =4/3 πR3 =4/3 π (ro A1/3)3
ρN = AmN /4/3 π (ro A1/3)3= mN /4/3 π ro3
Substituting the known values, the nuclear density is calculated as 1.816 × 1017 kg m−3 which is almost a constant for all the nuclei irrespective of its size.The high value of the nuclear density shows that the nuclear matter is in an extremely compressed state.
Nuclear charge
The charge of a nucleus is due to the protons present in it. Each proton has a positive charge equal to 1.6 × 10−19 C.
∴ The nuclear charge = Ze, where Z is the atomic number.
It is convenient to express the mass of a nucleus in atomic mass unit (amu), though the unit of mass is kg. One atomic mass unit is considered as one twelfth of the mass of carbon atom 6C12. Carbon of atomic number 6 and mass number 12 has mass equal to 12 amu.
1 amu = 1.66 × 10−27 kg
The mass of a proton, mp = 1.007276 amu
This is equal to the difference in mass of the hydrogen atom which is 1.007825 amu and the mass of electron.
The mass of a neutron, mn = 1.008665 amu
The energy equivalence of one amu can be calculated in electron-volt
Einstein’s mass energy relation is, E = mc2
Here, m = 1 amu = 1.66 × 10−27 kg ,c = 3 × 108 ms−1
∴ E = 1.66 × 10−27 × (3 × 108)2 J
One electron-volt (eV) is defined as the energy of an electron when
it is accelerated through a potential difference of 1 volt.
1 eV = 1.6 × 10−19 coulomb × 1 volt
1 eV = 1.6 × 10−19 joule
Hence E = [1.66 × 10−27 × (3 × 108)2 ] /1.6 × 10−19 = 931 × 106 eV
= 931 million electronvolt = 931 MeV
Thus, energy equivalent of 1 amu = 931 MeV
Nuclear mass:
As the nucleus contains protons and neutrons, the mass of the nucleus is assumed to be the mass of its constituents.
Assumed nuclear mass = ZmP + Nmn,
where mp and mn are the mass of a proton and a neutron respectively. However, from the measurement of mass by mass spectrometers, it is found that the mass of a stable nucleus (m) is less than the total mass of the nucleons.i.e mass of a nucleus, m < (Zmp + Nmn)
Zmp + Nmn – m = Δm
where Δm is the mass defect.Thus, the difference in the total mass of the nucleons and the actual mass of the nucleus is known as the mass defect.
Binding energy
When the protons and neutrons combine to form a nucleus, the mass that disappears (mass defect, Δm) is converted into an equivalent amount of energy (Δmc2). This energy is called the binding energy of the nucleus.
∴ Binding energy = [ZmP + Nmn – m] c2 = Δm c2
The binding energy of a nucleus determines its stability against disintegration. In other words, if the binding energy is large, the nucleus is stable and vice versa.
The binding energy per nucleon is BE/A=Binding energy of the nucleus/Total number of nucleons.
It is found that the binding energy per nucleon varies from element to element.A graph is plotted with the mass number A of the nucleus along the X−axis and binding energy per nucleon along the Y-axis.
– empirical mass formula - liquid drop model – Nuclear forces - Elements of two – body
problem – Charge independence and charge symmetry of nuclear forces - Evidence of
nuclear shell structure – Single particle shell model – Its validity and limitations – Collective
model –
Interactions of charged particles and e.m.rays with matter
Basic principles of
Interactions of charged particles and e.m.rays with matter
Basic principles of
Ionization chamber
Proportional counter
GM counter
Scintillation detectors
Semiconductor detectors
The ionization chamber used to measure the average number of ionizations per minute occurring within the gas. It is a gas-filled can (air) with a window at one end, two parallel plates (anode& cathode), a meter, and a battery.
The gas is most often at normal atmospheric pressure. A thin window at one end of the can admits radiation which ionizes the air. The current is measured by meter which is connected as shown the circuit.
Proportional counter
The proportional counter is similar to an ionization chamber. The filling gas is more likely to be argon or an argon–methane mixture than air, but the major difference between them is the higher voltage and the resulting gas amplification.
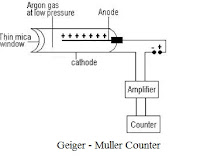
GM counter
The Geiger counter is an ionization chamber that operates at a relatively high applied voltage The chamber is usually filled with argon containing traces of other gases such as halogen or methane, although a detector will function with a filling as simple as dry air. The sensitive end of the probe is generally a mica window protected by an external metal mesh. When the radioactive radiations enter the GM tube through the mica window and ionises the argon gas. A pulse current is produced and counted by a counter.
Scintillation detectors
Scintillation detectors consist of a phosphor-coated screen and a photomultiplier tube. Radiation incident upon the phosphor produce photons in the ultraviolet part of the spectrum, which are amplified by the Photo Multiplier tube then output signal is fed to the electronic circuits.
Semiconductor detectors
The semiconductor detector most commonly used in the detection of gamma radiation is the germanium–lithium detector. This type of detector has been used in gamma radiation spectroscopy since the 1960.
Semiconductor detector has a PN junction with reverse bias. The interaction of Radiation with the semiconducting junction produces electron-hole pairs. These pairs are pulled by the electric field and that can be identified with proper electronics circuit.
Radioactive decays: Basic theoretical understanding
Radioactive decay is the process in which an unstable atomic nucleus spontaneously loses energy by emitting ionizing particles and radiation. This decay, or loss of energy, results in an atom of one type, called the parent nuclide transforming to an atom of a different type, named the daughter nuclide. For example: a carbon-14 atom (the "parent") emits radiation and transforms to a nitrogen-14 atom (the "daughter"). This is a random process on the atomic level, in that it is impossible to predict when a given atom will decay, but given a large number of similar atoms the decay rate, on average, is predictable.
α – decay :
When a nucleus undergoes alpha-decay, it transforms to a different nucleus by emitting an alpha-particle (a helium nucleus, 2He4). For example, when 92U 238 undergoes alpha-decay, it transforms to 90 Th 234
92U 238 → 90 Th 234 + 2He4
In this process, it is observed that since 4 2He contains two protons and two neutrons, the mass number and the atomic number of the daughter nucleus decreases by four and two, respectively. Thus, the transformation of a nucleus Z X A into a nucleus Z-2 YA-4 can be expressed as
Z X A → Z-2 YA-4 + 2He4
β - Decay :
When a radioactive nucleus disintegrates by emitting a β−particle, the atomic number increases by one and the mass number remains the same. β− decay can be expressed as
zXA → Z+1YA + −1e0
Example : Thorium (90Th234) is converted to protoactinium (91Pa234) due to β−decay
90Th234 → 91Pa234 + −1e0
At a time, either α or β−particle is emitted. Both α and β particles are not emitted during a single decay.
Gamma Ray Emission:
When a radioactive nucleus emits γ−rays, only the energy level of the nucleus changes and the atomic number and mass number remain the same. During α or β− decay, the daughter nucleus is mostly in the excited state. It comes to ground state with the emission of γ−rays. Example : During the radioactive disintegration of radium (88Ra226) into radon (86Rn222), gamma ray of energy 0.187 MeV is emitted, when radon returns from the excited state to the ground state .
Positron decay:
Positron emission involves the conversion of a proton in the nucleus into a neutron plus an ejected positron, or +. A positron has the same mass as an electron, but the opposite charge. The result of positron emission is a decrease in the atomic number of the product, but no change in the mass number.
Electron capture:
Electron Capture is a process in which the nucleus captures an inner-shell electron, thereby converting a proton into a neutron. The mass number of the product nucleus is unchanged, but the atomic number decreases by one.
80 Hg 117 +-1 e 0 → 79 Au 197
Nuclear reactions – Elementary ideas of reaction mechanism – Compound nucleus and
direct reactions – Elementary ideas of fission and fusion – Particle Physics: Symmetries and
Conservation laws –Classification of fundamental forces and elementary particles – Iso-spin
– Strangeness- Gell-Mann Nishijima formula – Quark model – C.P.T.invariance in different
interactions – Parity nonconservation in weak interaction.